FlashAttention：具有 IO 感知，快速且内存高效的新型注意力算法

Vachel October 19, 2023

Transformer 模型的核心是自注意力机制（self attention），其在序列长度上时间和存储的复杂度都在 $O(N^2)$ 级别。随着大语言模型（LLMs）规模的不断扩大，为 LLM 配备更长的上下文背景，在工程实现上面临着非常大的挑战。

来自斯坦福大学计算机系与纽约州立大学布法罗分校的科研团队发表了一种新型的注意力算法，名叫 FlashAttention ，其不仅拥有比 PyTorch 标准注意力快 2~4 倍的运行速度，所需内存还减少了 5~20 倍。后续发布的 FlashAttention2，Flash Decoding 还拥有更夸张的性能加速表现。

幻方深度求索研发的大模型训练工具 HAI-LLM 全系采用 FlashAttention，大幅提高显卡利用率，实现了非常优异的训练表现。本系列文章将为大家深入浅出聊聊 FlashAttention 背后的技术和我们的实践经验。

论文地址：https://arxiv.org/abs/2205.14135

项目源码：https://github.com/Dao-AILab/flash-attention

背景

传统的注意力算法其内存效率是 $O(N^2)$ 的。过去一些优化注意力机制的方法是采用近似值，例如稀疏近似、低秩近似以及它们的组合。尽管这些方法可以将计算降低到线性或接近线性（ $O(N)$ ），但它们过于关注降低每秒所执行的浮点运算次数（FLops），并且倾向于忽略来自内存访问（IO）的开销。

多年来 GPU FLOPS 的增长速度一直比内存吞吐量（TB/s）的增长更快。我们在 A100 或同级别显卡上优化模型训练的实践中发现，内存吞吐量才是影响训练进一步提效的重要瓶颈。FLOPS 和内存吞吐量需要紧密结合，才能充分提高的训练效率。这就需要我们在软件层面上进行更加细致的设计。

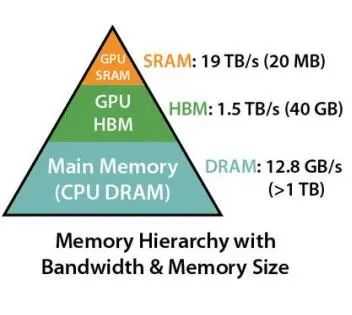
如下图所示：

上图展示了 CPU 和 GPU 不同层级内存的吞吐量和容量。可以看到内存不是一个单一的部件，它在本质上是分层的，一般的规则是：内存越快，越昂贵，容量越小。

以 A100 为例：A100 GPU 有 40~80GB 的高带宽内存（HBM），带宽为 1.5-2.0 TB/s，而每 108 个流处理器有 192KB 的 SRAM，带宽估计在 19TB/s 左右。可以看到虽然 SRAM 容量小了很多，但是速度却提升了10倍，所以如何高效的利用 SRAM 是提速注意力算法的关键。

标准注意力算法

我们首先看看标准注意力算法背后的计算逻辑：

可以看到标准注意力算法基本上将 HBM 加载/存储操作视为0成本（它并不能感知 IO）。

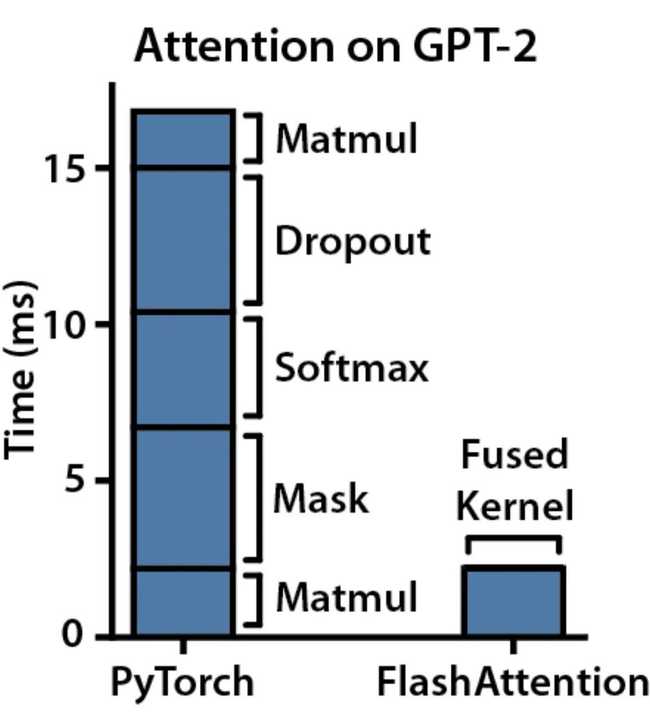
下图展示了 GPT-2 模型中一个 Attention 算子的完整计算耗时统计：

可以看到，masking，softmax 和 dropout 操作占用了大量时间，而主要利用 FLOPS 的矩阵乘法（Matmul）却只占用了一部分时间。因此，感知硬件 IO 进行优化的 FlashAttention 算法被提出，其可以大幅减少冗余的 HBM IO 并充分利用 SRAM 进行计算加速。

FlashAttention

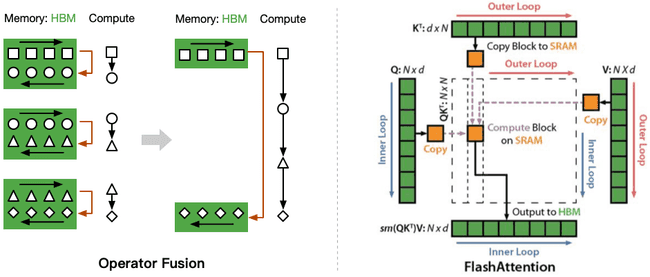
FlashAttention 思路是：既然标准注意力算法要将 S 写回 HBM，而这个步骤只为了重新加载计算 Softmax，那么我们可以将其保存在 SRAM 中，等执行完所有中间步骤后，再将最终结果写回 HBM。如下图所示：

可以看到 FlashAttention 将多个操作融合在一起，其只从 HBM 加载一次，执行融合的算子操作，然后将结果写回 HBM。融合操作主要采用了如下两种技术：

Tiling：矩阵分块计算，在不访问整个输入的情况下计算 Softmax 函数的缩减，在前向和后向传播时都使用；
Recomputation：时间换空间，不存储中间注意力矩阵而采用重计算的方式，仅在后向传播时使用。

完整的伪代码如下：

1. Tiling 分块计算

对于有限的 SRAM 容量， $N^2$ 的存储用量使得序列长度（N）限定在了一定范围，因此我们要进行矩阵分块计算。对于矩阵乘法与逐点操作（scale，masking，dropout）的分块计算是比较容易实现的，主要障碍是 Softmax 函数，因为其需要将所有的分数列耦合在一起。为此研究者使用了一个技巧：既然 Softmax 与注意力 $\mathbf{K}$ 的列是耦合的，通过引入了两个额外的统计量 $m(x),l(x)$ 来进行解耦，实现了分块计算。具体如下：

$m(x):=\max_i x_i, ~~f(x):=[e^{x_i-m(x)}...e^{x_B-m(x)}], ~~l(x):=\sum_i f(x)_i, ~~softmax(x):=\frac{f(x)}{l(x)}$

对于两个向量 $x^{(1)},x^{(2)}\in R^B$ ，解耦拼接向量 $x=[x^{(1)},x^{(2)}]\in R^{2B}$ 的 Softmax 计算：

$m(x)=m([x^{(1)},x^{(2)}])=\max(x^{(1)},x^{(2)}), f(x)=[e^{m(x^{(1)})-m(x)}f(x^{(1)}) ~~ e^{m(x^{(2)})-m(x)}f(x^{(2)})]$ $l(x)=l([x^{(1)},x^{(2)}])=e^{m(x^{(1)})-m(x)}l(x^{(1)}) + e^{m(x^{(2)})-m(x)}l(x^{(2)}), ~~ softmax(x)=\frac{f(x)}{l(x)}$

需要注意的是，可以利用 GPU 多线程同时并行计算多个块的 Softmax。为了充分利用硬件性能，多个块的计算不是串行的，而是并行。

2. 重计算

为了避免产生冗余的 HBM 读写次数，FlashAttention 没有为后向传递保存很大的中间结果矩阵。

在标准注意力实现中，后向传递计算 Q,K,V 的梯度时，需要用到 NxN 的中间矩阵 S,P ，但这两个矩阵并没有保存下来。研究用的技巧是重计算，保存了两个统计量 $m(x),l(x)$ ，后向传递时在高速的 SRAM 上快速地重新计算，通过分块的方式重新计算出注意力矩阵 S,P 。这种方式比标准方法要快很多。

实验

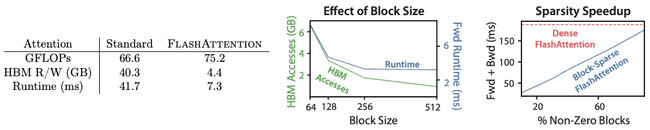
相比于标准的注意力算法，FlashAttention 虽然由于反向传播需要重新计算导致 GFLOPs 增加，但是 FlashAttention 有效减少了 HBM 的 I/O ，运行时间显著减少，如下图左所示：

同时从上图右也可以看到，随着 Block Size 增大，HBM 的访问次数减少，运行时间也随之减少。当 Block Size 超过256 时，尽管 HBM 访问次数在减少，但运行时间并没有减少。这时性能受到了其他因素的限制，例如，计算受限。另外需要注意的是，更大的 Block Size 可能会导致执行一次融合算子操作需要的显存超出 SRAM 的大小。

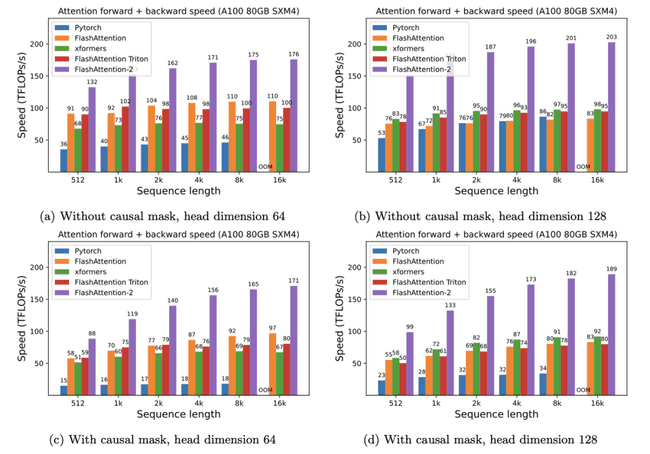
在 A100 显卡上进行实验，FlashAttention 的加速效果如下图所示：

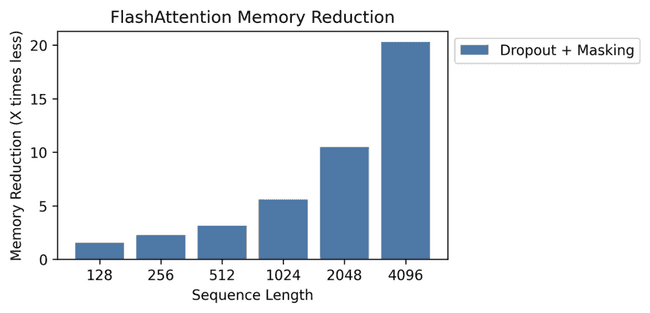
内存的变化为：

可以看到，在不同的序列长度下组合 dropout 和 masking，都有不同程度的加速效果；随着序列长度的增加，FlashAttention 对于内存消耗有着不断优化的效果。

总结

多数大语言模型输入输出的最大序列长度只有 2K 或 4K，本质原因是 transformer 的核心组件 self-attention 块的计算复杂度和空间复杂度是 $O(N^2)$ 的。FlashAttention 的成功启发我们，可以通过分块计算、算子融合和重计算技术，实现深度学习模型的优化与加速，这对于AI工业实践走向深水区有很大的借鉴意义。